As the demand for both greater arithmetic density and computational accuracy grows, number systems will play an increasingly pivotal role in the design of next-generation computing platforms. There are vast opportunities to explore the algorithm-architecture co-design of novel number systems that provide greater amortization of the PPA costs that scale with arithmetic density, and most importantly, without compromising on computational accuracy. Below is a short summary of my relevant work on this topic so far.

Emerging AI models exhibit a parameter distribution spread that far exceeds the dynamic range of commonly-used low-precision data types. Realizing the need for adaptive tensor scaling, we proposed the best paper award-winning number system called AdaptivFloat, which informs a generalized floating-point based mathematical blueprint for adaptive and resilient DNN quantization, and that can be easily applied on neural models of various categories (CNN, RNN, Transformers), and parameter statistics.

In essence, AdaptivFloat introduces in its exponent field an exponent bias that is computed from the maximum absolute value in a given tensor. This allows the datatype to dynamically shift, at a layer, channel, or vector granularity – its representation range in order to cater to the most impactful parameters in a DNN’s weight, activation, or gradient tensor.

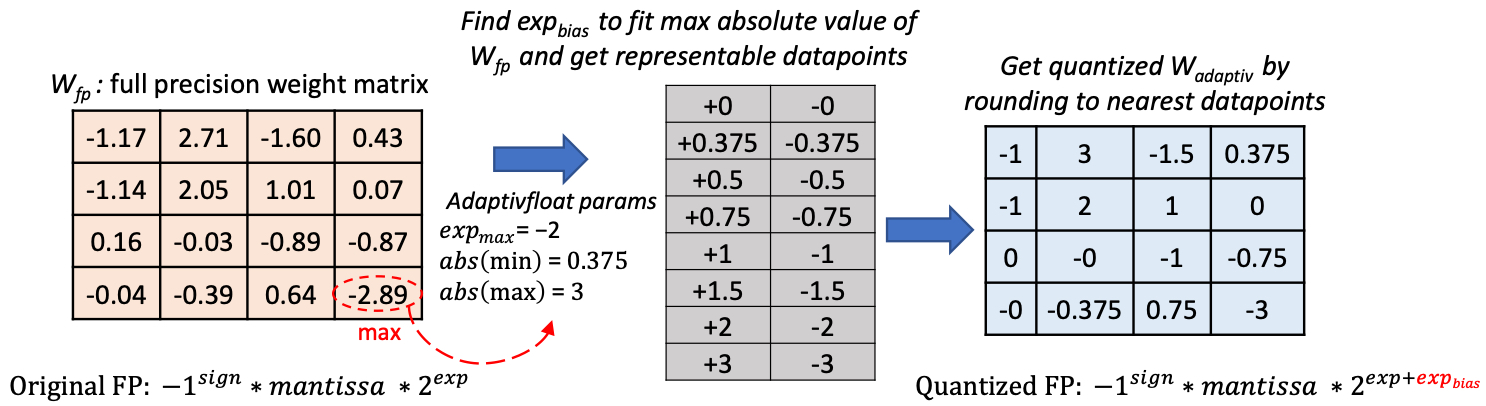
AdaptivFloat quantization scheme based on exponential bias shift from maximum absolute tensor value.

To facilitate the exploration of newer number formats in the context of deep learning and other emerging applications, we developed and open-sourced GoldenEye, a number format simulator that enables the selection of configurable number systems as a first-order parameter when evaluating their impact on DNN classification accuracy.

We further demonstrated how the number system and the underlying hardware can be optimally co-designed for reconfigurable architectures, and for domain-specific applications such as robotics.